Bonjour,
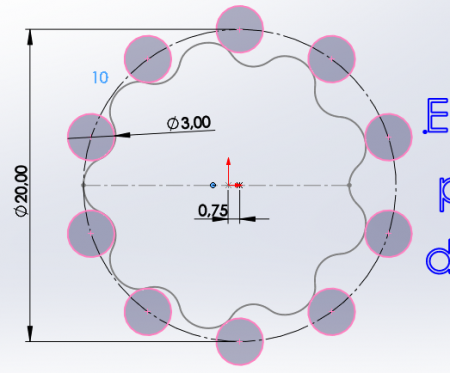
J'ai besoin de réalisé un réducteur à partir de cycloides.
J'ai mon équation en fonction du temps qui reprendra ici la valeur en radian.
Voir ma pièce jointe de la géométrie.
Je voudrai utiliser les équations (fonction de Solidworks avec des variables qui reprendront mes données initiales)
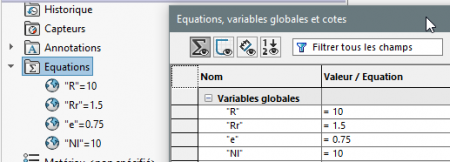
Voici mon paramétrage sur les deux équations paramétrées
X = (R*cos(t))-(Rr*cos(t+arctan(sin((1-N)*t)/((R/EN)-cos((1-N)*t)))))-(E*cos(N*t))
Y = (-R*sin(t))+(Rr*sin(t+arctan(sin((1-N)*t)/((R/EN)-cos((1-N)*t)))))+(E*sin(N*t))
paramètrage de l'équation en fonction de t.
R= 10, E = 0.75, Rr = 1.5, N = 10 ma base de test .
=(10*cos(t))-(1.5*cos(t+arctan(sin((1-10)*t)/((10/0.75*10)-cos((1-10)*t)))))-(0.75*cos(10*t)) en remplaçant les paramètres.
formule à saisir pour la composante de X(t)
(10*cos(t))-(1.5*cos(t+arctan(sin(-9*t)/((4/3)-cos(-9*t)))))-(0.75*cos(10*t))
formule à saisir pour la composante de Y(t)
(-10*sin(t))+(1.5*sin(t+arctan(sin(-9*t)/((4/3)-cos(-9*t)))))+(0.75*sin(10*t))
je balaye de 0 à pi.
Merci pour votre aide.Bonne journée.
Spectrum.
ma_base_a_partir_de_lequation_parametree.jpg